Consider a road with two cars at a distance of 100 kilometers which are driving towards each other. The left car drives at a speed of forty kilometers per hour and right car at a speed of sixty kilometers per hour. A bird starts from the location of right car and flies at a speed of 80 kilometers per hour. When it reaches the left car, it turns its direction, and when it reaches the right car, it turns its direction again to the opposite, etc. Check the figure for the details
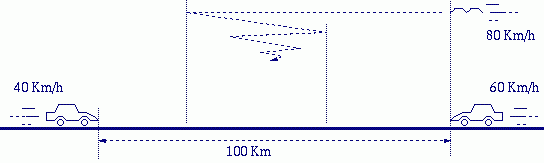
Now the question is what is the total distance that the bird has traveled at the moment that the two cars have reached each other?
